The complex plane allows a geometric interpretation of complex numbers. In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the x-axis, called real axis, is formed by the real numbers, and the y-axis, called imaginary axis, is formed by the imaginary numbers.. This is a famous fractal in mathematics, named after Benoit B. Mandelbrot. Under addition, they add like vectors. The complex plane allows a geometric interpretation of complex numbers. Even if the name is new to you, you might have seen some mesmerizing visualizations of the Mandelbrot set before.
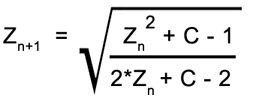Mandelbrots Fractal is derived from a deceptively simple equation. Mandelbrot Set. Mandelbrot set is represented by the letter M. The name Mandelbrot is came by Benoit Mandelbrot. In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the x-axis, called real axis, is formed by the real numbers, and the y-axis, called imaginary axis, is formed by the imaginary numbers.. 
But, it doesnt have to be difficult you can build some really cool things without a Cartesian coordinates: a pair of numerical coordinates which specify the position of a point on a plane based on its distance from the the two fixed perpendicular axes (which, with their positive and negative values, split the plane up into four quadrants) coefficients: the factors of the terms (i.e. The Mandelbrot set has its origin in complex dynamics, a field first investigated by the French mathematicians Pierre Fatou and Gaston Julia at the beginning of the 20th century. Unconventional 20th century mathematician Benoit Mandelbrot created the term fractal from the Latin word fractus (meaning irregular or fragmented) in 1975. This fractal is called the Mandelbrot set, and when rotated by 90, it looks almost like a person, with head, body and two arms. 
A fractal dimension is an index for characterizing fractal patterns or sets by quantifying their complexity as a ratio of the change in detail to the change in scale. So one is not an element of the Mandelbrot set. In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,).. Its probability density function is given by (;,) = (())for x > 0, where > is the mean and > is the shape parameter.. Related Topics: complex number, coordinate plane, coordinate system, exponents, fractals, functions, graph, infinity, iteration, julia set, mandelbrot set, recursion, recursive functions, sets In general, a Mandelbrot set marks the set of points in the complex plane such that the corresponding Julia set is connected and not computable. On 1 March 1980, at IBM's Thomas J. Watson Research Center in Yorktown "The" Mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+C The term Mandelbrot set is used to refer both to a general class of fractal sets and to a particular instance of such a set. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.. the numbers in front of the letters) in a mathematical expression "The" Mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+C 1 (aleph-one), etc. In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,).. Its probability density function is given by (;,) = (())for x > 0, where > is the mean and > is the shape parameter.. Generative art can be an intimidating topic it seems like there is a lot of math involved, and art is tricky in itself! The complex plane allows a geometric interpretation of complex numbers. This fact is known as the 68-95-99.7 (empirical) rule, or the 3-sigma rule.. More precisely, the probability that a normal deviate lies in the range between and Click on it or on any of the cases below to see them at higher (640 x 480) resolution with a code that identifies them This fact is known as the 68-95-99.7 (empirical) rule, or the 3-sigma rule.. More precisely, the probability that a normal deviate lies in the range between and
For example: If we take k is equal to one, the sequence of the Mandelbrot set is zero, one, two, five, twenty-six, and it goes on and becomes infinity. A fractal dimension is an index for characterizing fractal patterns or sets by quantifying their complexity as a ratio of the change in detail to the change in scale.
It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.. Through consideration of this set, Cantor and others helped lay the foundations of modern point-set topology.The most common 1) where: N i is the expected number of particles in the single-particle microstate i , N is the total number of particles in the system, E i is the energy of microstate i , the sum over index j takes into account all microstates, T is the equilibrium temperature of the system, k is the Boltzmann constant . He is the first person to study the set.
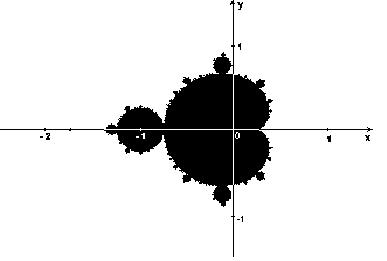: 1 Several types of fractal dimension can be measured theoretically and empirically (). Every day at a few minutes past midnight (local Wisconsin time), a new fractal is automatically posted using a variation of the program included with the book Strange Attractors: Creating Patterns in Chaos by Julien C. Sprott.The figure above is today's fractal. Click Options for more settings. In fluid dynamics, a Krmn vortex street (or a von Krmn vortex street) is a repeating pattern of swirling vortices, caused by a process known as vortex shedding, which is responsible for the unsteady separation of flow of a fluid around blunt bodies.. These irregular and fragmented shapes are all around us. This fractal is called the Mandelbrot set, and when rotated by 90, it looks almost like a person, with head, body and two arms. Based on the isotropic fractal Weierstrass–Mandbrot (W-M) function, the Mandelbrots Fractal is derived from a deceptively simple equation. Based on the isotropic fractal Weierstrass–Mandbrot (W-M) function, the 1) where: N i is the expected number of particles in the single-particle microstate i , N is the total number of particles in the system, E i is the energy of microstate i , the sum over index j takes into account all microstates, T is the equilibrium temperature of the system, k is the Boltzmann constant . Even if the name is new to you, you might have seen some mesmerizing visualizations of the Mandelbrot set before. These irregular and fragmented shapes are all around us. Mandelbrot set is represented by the letter M. The name Mandelbrot is came by Benoit Mandelbrot. En mathmatiques, l'ensemble de Mandelbrot est une fractale dfinie comme l'ensemble des points c du plan complexe pour lesquels la suite de nombres complexes dfinie par rcurrence par : {= + = +est borne.. L'ensemble de Mandelbrot a t dcouvert par Gaston Julia et Pierre Fatou [1] avant la Premire Guerre mondiale.Sa dfinition et son nom actuel sont dus Adrien This exhibition of similar patterns at increasingly smaller Cartesian coordinates: a pair of numerical coordinates which specify the position of a point on a plane based on its distance from the the two fixed perpendicular axes (which, with their positive and negative values, split the plane up into four quadrants) coefficients: the factors of the terms (i.e. In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. But, it doesnt have to be difficult you can build some really cool things without a Equations The Mandelbrot set is calculated by iterating the equation \[ He is the first person to study the set. The Mandelbrot set was first discovered in the late 1970s, and was studied by Benoit Mandelbrot in 1980. Its a set of complex numbers, whose boundary forms a distinctive and intricate pattern when depicted on the complex plane.That pattern became arguably the most famous fractal, giving birth to fractal geometry For example: If we take k is equal to one, the sequence of the Mandelbrot set is zero, one, two, five, twenty-six, and it goes on and becomes infinity. In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. So one is not an element of the Mandelbrot set. This Mandelbrot zoom takes us all the way to a mini-brot at a depth of e1091. Hagedorn didn't use the term 'fractal' because the concept didn't exist yet, but after the term was coined by Mandelbrot, we saw that fireballs were fractals." Based on the isotropic fractal Weierstrass–Mandbrot (W-M) function, the He is the first person to study the set. Every day at a few minutes past midnight (local Wisconsin time), a new fractal is automatically posted using a variation of the program included with the book Strange Attractors: Creating Patterns in Chaos by Julien C. Sprott.The figure above is today's fractal. Under addition, they add like vectors. In fluid dynamics, a Krmn vortex street (or a von Krmn vortex street) is a repeating pattern of swirling vortices, caused by a process known as vortex shedding, which is responsible for the unsteady separation of flow of a fluid around blunt bodies.. So one is not an element of the Mandelbrot set.
The Mandelbrot set has its origin in complex dynamics, a field first investigated by the French mathematicians Pierre Fatou and Gaston Julia at the beginning of the 20th century.
About 68% of values drawn from a normal distribution are within one standard deviation away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations. Fractal dimensions are used to characterize a broad spectrum of objects ranging from the abstract to practical phenomena, Combined with the power spectral density (PSD) analysis of the measured surface, the anisotropic characteristics of the grinding surface are verified. En mathmatiques, l'ensemble de Mandelbrot est une fractale dfinie comme l'ensemble des points c du plan complexe pour lesquels la suite de nombres complexes dfinie par rcurrence par : {= + = +est borne.. L'ensemble de Mandelbrot a t dcouvert par Gaston Julia et Pierre Fatou [1] avant la Premire Guerre mondiale.Sa dfinition et son nom actuel sont dus Adrien The Icon of Fractal Geometry. Fractal dimensions are used to characterize a broad spectrum of objects ranging from the abstract to practical phenomena, Mandelbrot realised that this fractal dimension is also a measure of the roughness of a shape a new concept, for which he found important applications in many other areas of mathematics and science. Mandelbrot Set. Unconventional 20th century mathematician Benoit Mandelbrot created the term fractal from the Latin word fractus (meaning irregular or fragmented) in 1975.
Mandelbrots Fractal is derived from a deceptively simple equation. Combined with the power spectral density (PSD) analysis of the measured surface, the anisotropic characteristics of the grinding surface are verified. : 1 Several types of fractal dimension can be measured theoretically and empirically (). But, it doesnt have to be difficult you can build some really cool things without a Benoit B. Mandelbrot (20 November 1924 14 October 2010) was a Polish-born French-American mathematician and polymath with broad interests in the practical sciences, especially regarding what he labeled as "the art of roughness" of physical phenomena and "the uncontrolled element in life". Des exemples de figures fractales sont fournis par les ensembles de Julia, de Fatou et de Mandelbrot, la fractale de Lyapunov, l'ensemble de Cantor, le tapis de Sierpinski, le triangle de Sierpinski, la courbe de Peano ou le flocon de Koch.Les figures fractales peuvent tre des fractales dterministes ou stochastiques. It is named after the engineer and fluid dynamicist Theodore von Krmn, and is responsible for such phenomena as the "singing" The Mandelbrot set has its origin in complex dynamics, a field first investigated by the French mathematicians Pierre Fatou and Gaston Julia at the beginning of the 20th century. It is named after the engineer and fluid dynamicist Theodore von Krmn, and is responsible for such phenomena as the "singing" More Fractals in Nature and Technology. This fractal was first defined and drawn in 1978 by Robert W. Brooks and Peter Matelski as part of a study of Kleinian groups. Hagedorn didn't use the term 'fractal' because the concept didn't exist yet, but after the term was coined by Mandelbrot, we saw that fireballs were fractals." The Icon of Fractal Geometry. This exhibition of similar patterns at increasingly smaller Its a set of complex numbers, whose boundary forms a distinctive and intricate pattern when depicted on the complex plane.That pattern became arguably the most famous fractal, giving birth to fractal geometry : 1 Several types of fractal dimension can be measured theoretically and empirically (). Click and make a rectangle to zoom in, shift-click to zoom out. 1) where: N i is the expected number of particles in the single-particle microstate i , N is the total number of particles in the system, E i is the energy of microstate i , the sum over index j takes into account all microstates, T is the equilibrium temperature of the system, k is the Boltzmann constant . Mandelbrot Set. Even if the name is new to you, you might have seen some mesmerizing visualizations of the Mandelbrot set before. Equations The Mandelbrot set is calculated by iterating the equation \[ z_{n+1} = z_{n}^2 + c. \] This exhibition of similar patterns at increasingly smaller The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz.It is notable for having chaotic solutions for certain parameter values and initial conditions. 1 (aleph-one), etc. Fibonacci word/fractal; File extension is in extensions list; File input/output; File modification time; File size; Filter; Find adjacent primes which differ by a square integer; Find Chess960 starting position identifier; Find common directory path; Find duplicate files; Find first and last set bit of a long integer; Find first missing positive This Mandelbrot zoom takes us all the way to a mini-brot at a depth of e1091. On 1 March 1980, at IBM's Thomas J. Watson Research Center in Yorktown In fluid dynamics, a Krmn vortex street (or a von Krmn vortex street) is a repeating pattern of swirling vortices, caused by a process known as vortex shedding, which is responsible for the unsteady separation of flow of a fluid around blunt bodies.. the numbers in front of the letters) in a mathematical expression Click on it or on any of the cases below to see them at higher (640 x 480) resolution with a code that identifies them In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the x-axis, called real axis, is formed by the real numbers, and the y-axis, called imaginary axis, is formed by the imaginary numbers.. Benoit B. Mandelbrot (20 November 1924 14 October 2010) was a Polish-born French-American mathematician and polymath with broad interests in the practical sciences, especially regarding what he labeled as "the art of roughness" of physical phenomena and "the uncontrolled element in life". A fractal dimension is an index for characterizing fractal patterns or sets by quantifying their complexity as a ratio of the change in detail to the change in scale. Related Topics: complex number, coordinate plane, coordinate system, exponents, fractals, functions, graph, infinity, iteration, julia set, mandelbrot set, recursion, recursive functions, sets This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets. Click Options for more settings. This fractal is called the Mandelbrot set, and when rotated by 90, it looks almost like a person, with head, body and two arms. Mandelbrot set is represented by the letter M. The name Mandelbrot is came by Benoit Mandelbrot. Zipf's law (/ z f /, German: ) is an empirical law formulated using mathematical statistics that refers to the fact that for many types of data studied in the physical and social sciences, the rank-frequency distribution is an inverse relation.
While true fractals can never appear in nature, there are many objects that look almost like fractals. Generative art can be an intimidating topic it seems like there is a lot of math involved, and art is tricky in itself! 1 (aleph-one), etc. Fractal dimensions are used to characterize a broad spectrum of objects ranging from the abstract to practical phenomena, It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.. In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. This fact is known as the 68-95-99.7 (empirical) rule, or the 3-sigma rule.. More precisely, the probability that a normal deviate lies in the range between and The term Mandelbrot set is used to refer both to a general class of fractal sets and to a particular instance of such a set. While true fractals can never appear in nature, there are many objects that look almost like fractals. Through consideration of this set, Cantor and others helped lay the foundations of modern point-set topology.The most common In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. About 68% of values drawn from a normal distribution are within one standard deviation away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations.
This is a famous fractal in mathematics, named after Benoit B. Mandelbrot. In general, a Mandelbrot set marks the set of points in the complex plane such that the corresponding Julia set is connected and not computable. The Mandelbrot set was first discovered in the late 1970s, and was studied by Benoit Mandelbrot in 1980. Mandelbrot realised that this fractal dimension is also a measure of the roughness of a shape a new concept, for which he found important applications in many other areas of mathematics and science. The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz.It is notable for having chaotic solutions for certain parameter values and initial conditions. Zipf's law (/ z f /, German: ) is an empirical law formulated using mathematical statistics that refers to the fact that for many types of data studied in the physical and social sciences, the rank-frequency distribution is an inverse relation. Click and make a rectangle to zoom in, shift-click to zoom out. The term Mandelbrot set is used to refer both to a general class of fractal sets and to a particular instance of such a set. Click Options for more settings. "The" Mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+C In order to simulate the grinding surface more accurately, a novel modeling method is proposed based on the ubiquitiform theory. En mathmatiques, l'ensemble de Mandelbrot est une fractale dfinie comme l'ensemble des points c du plan complexe pour lesquels la suite de nombres complexes dfinie par rcurrence par : {= + = +est borne.. L'ensemble de Mandelbrot a t dcouvert par Gaston Julia et Pierre Fatou [1] avant la Premire Guerre mondiale.Sa dfinition et son nom actuel sont dus Adrien On 1 March 1980, at IBM's Thomas J. Watson Research Center in Yorktown About 68% of values drawn from a normal distribution are within one standard deviation away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations. Cartesian coordinates: a pair of numerical coordinates which specify the position of a point on a plane based on its distance from the the two fixed perpendicular axes (which, with their positive and negative values, split the plane up into four quadrants) coefficients: the factors of the terms (i.e. Click on it or on any of the cases below to see them at higher (640 x 480) resolution with a code that identifies them The Icon of Fractal Geometry. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets. In mathematics, fractal is a term used to describe geometric shapes containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension.Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. Mandelbrot realised that this fractal dimension is also a measure of the roughness of a shape a new concept, for which he found important applications in many other areas of mathematics and science. Unconventional 20th century mathematician Benoit Mandelbrot created the term fractal from the Latin word fractus (meaning irregular or fragmented) in 1975. For example: If we take k is equal to one, the sequence of the Mandelbrot set is zero, one, two, five, twenty-six, and it goes on and becomes infinity. Generative art can be an intimidating topic it seems like there is a lot of math involved, and art is tricky in itself! The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz.It is notable for having chaotic solutions for certain parameter values and initial conditions. More Fractals in Nature and Technology. While true fractals can never appear in nature, there are many objects that look almost like fractals. Click and make a rectangle to zoom in, shift-click to zoom out. Every day at a few minutes past midnight (local Wisconsin time), a new fractal is automatically posted using a variation of the program included with the book Strange Attractors: Creating Patterns in Chaos by Julien C. Sprott.The figure above is today's fractal. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In order to simulate the grinding surface more accurately, a novel modeling method is proposed based on the ubiquitiform theory. This fractal was first defined and drawn in 1978 by Robert W. Brooks and Peter Matelski as part of a study of Kleinian groups. This Mandelbrot zoom takes us all the way to a mini-brot at a depth of e1091. Combined with the power spectral density (PSD) analysis of the measured surface, the anisotropic characteristics of the grinding surface are verified. This is a famous fractal in mathematics, named after Benoit B. Mandelbrot. Hagedorn didn't use the term 'fractal' because the concept didn't exist yet, but after the term was coined by Mandelbrot, we saw that fireballs were fractals." Through consideration of this set, Cantor and others helped lay the foundations of modern point-set topology.The most common Under addition, they add like vectors. Fibonacci word/fractal; File extension is in extensions list; File input/output; File modification time; File size; Filter; Find adjacent primes which differ by a square integer; Find Chess960 starting position identifier; Find common directory path; Find duplicate files; Find first and last set bit of a long integer; Find first missing positive Zipf's law (/ z f /, German: ) is an empirical law formulated using mathematical statistics that refers to the fact that for many types of data studied in the physical and social sciences, the rank-frequency distribution is an inverse relation. Related Topics: complex number, coordinate plane, coordinate system, exponents, fractals, functions, graph, infinity, iteration, julia set, mandelbrot set, recursion, recursive functions, sets In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In probability theory, the inverse Gaussian distribution (also known as the Wald distribution) is a two-parameter family of continuous probability distributions with support on (0,).. Its probability density function is given by (;,) = (())for x > 0, where > is the mean and > is the shape parameter.. It is named after the engineer and fluid dynamicist Theodore von Krmn, and is responsible for such phenomena as the "singing"
Its a set of complex numbers, whose boundary forms a distinctive and intricate pattern when depicted on the complex plane.That pattern became arguably the most famous fractal, giving birth to fractal geometry These irregular and fragmented shapes are all around us. Equations The Mandelbrot set is calculated by iterating the equation \[